How Long Until at Rest Again Math Problem

Math Models

29 Solve Compatible Motion Applications

Learning Objectives

By the cease of this section, you will be able to:

Solve uniform motion applications

Before you get started, take this readiness quiz.

Discover the altitude travelled past a car going 70 miles per hour for 3 hours.
If yous missed this problem, review (Figure).
Solve $x+1.2\left(x-10\right)=98.$
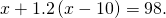
If you missed this problem, review (Figure).
Convert 90 minutes to hours.
If you missed this trouble, review (Figure).

Solve Uniform Motility Applications

When planning a road trip, information technology often helps to know how long it volition take to reach the destination or how far to travel each day. We would apply the altitude, charge per unit, and time formula, $D=rt,$ which we have already seen.

In this section, we will use this formula in situations that require a fiddling more than algebra to solve than the ones we saw before. By and large, we volition be looking at comparison two scenarios, such as two vehicles travelling at different rates or in opposite directions. When the speed of each vehicle is constant, nosotros telephone call applications similar this compatible motion problems.

Our problem-solving strategies will still apply here, but we volition add together to the starting time step. The first step will include drawing a diagram that shows what is happening in the instance. Drawing the diagram helps us understand what is happening and then that we will write an advisable equation. Then we will make a tabular array to organize the data, like we did for the money applications.

The steps are listed here for easy reference:

Use a Trouble-Solving Strategy in Distance, Charge per unit, and Time Applications.

Read the problem. Make sure all the words and ideas are understood.
- Draw a diagram to illustrate what information technology happening.
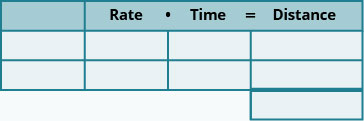
- Create a table to organize the information.
- Label the columns rate, time, distance.
- List the two scenarios.
- Write in the data you know.
Identify what nosotros are looking for.
Name what we are looking for. Cull a variable to represent that quantity.
- Complete the chart.
- Utilise variable expressions to represent that quantity in each row.
- Multiply the rate times the time to go the altitude.
Translate into an equation.
- Restate the problem in one sentence with all the important information.
- Then, translate the sentence into an equation.
Solve the equation using expert algebra techniques.
Cheque the answer in the problem and brand sure it makes sense.
Answer the question with a consummate sentence.

An express train and a local train exit Pittsburgh to travel to Washington, D.C. The limited railroad train can make the trip in 4 hours and the local train takes 5 hours for the trip. The speed of the express train is 12 miles per hour faster than the speed of the local train. Find the speed of both trains.

Solution

Step 1. Read the problem. Make sure all the words and ideas are understood.

Step two. Place what we are looking for.

Nosotros are asked to find the speed of both trains.
Observe that the altitude formula uses the word "rate," merely it is more than common to use "speed" when we talk nigh vehicles in everyday English.

Step 3. Name what we are looking for. Choose a variable to represent that quantity.

Complete the chart
Use variable expressions to represent that quantity in each row.
We are looking for the speed of the trains. Let's permit r represent the speed of the local train. Since the speed of the limited train is 12 mph faster, nosotros represent that as $r+12.$

$\begin{array}{ccc}\hfill r& =\hfill & \text{speed of the local train}\hfill \\ \hfill r+12& =\hfill & \text{speed of the express train}\hfill \end{array}$

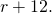
Fill in the speeds into the chart.

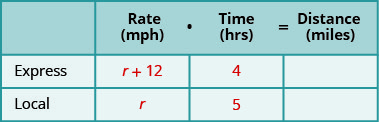
A table with three rows and four columns. The first row is a header row and reads from left to right _____, Rate (mph), Time (hrs), and Distance (miles). Below the blank header cell, we have Express and then Local. Below the Rate header cell, we have r plus 12 and then r. Below the Time header cell, we have 4 and then 5. The rest of the cells are blank.

Multiply the charge per unit times the fourth dimension to get the altitude.

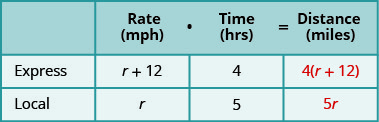
Step 4. Translate into an equation.

Restate the trouble in ane judgement with all the of import information.
Then, interpret the sentence into an equation.
The equation to model this situation will come from the relation between the distances. Look at the diagram we drew above. How is the distance travelled by the limited train related to the distance travelled by the local train?
Since both trains leave from Pittsburgh and travel to Washington, D.C. they travel the same altitude. So we write:

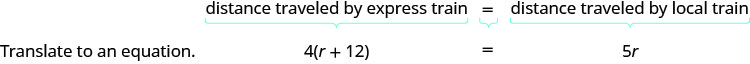
The sentence,

Stride v. Solve the equation using skilful algebra techniques.

Now solve this equation.	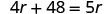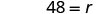And then the speed of the local railroad train is 48 mph.
Find the speed of the express train.	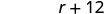The speed of the limited train is threescore mph.

Step 6. Check the answer in the problem and brand sure it makes sense.

express train	$\text{60 mph (4 hours) = 240 miles}$
local train	$\text{48 mph (5 hours) = 240 miles ✓}$

Step 7. Reply the question with a complete sentence.

The speed of the local railroad train is 48 mph and the speed of the express train is 60 mph.

Wayne and Dennis like to ride the wheel path from Riverside Park to the embankment. Dennis's speed is vii miles per hour faster than Wayne's speed, so information technology takes Wayne two hours to ride to the beach while it takes Dennis 1.v hours for the ride. Observe the speed of both bikers.

Wayne 21 mph, Dennis 28 mph

Jeromy can drive from his business firm in Cleveland to his college in Chicago in 4.five hours. It takes his mother 6 hours to make the aforementioned drive. Jeromy drives xx miles per hour faster than his mother. Discover Jeromy's speed and his mother'due south speed.

Jeromy fourscore mph, mother sixty mph

In (Figure), the last case, we had ii trains traveling the same altitude. The diagram and the nautical chart helped united states write the equation we solved. Let's see how this works in another case.

Christopher and his parents live 115 miles autonomously. They met at a restaurant between their homes to celebrate his mother'due south birthday. Christopher drove ane.5 hours while his parents drove i hour to become to the eating place. Christopher'due south average speed was 10 miles per hour faster than his parents' boilerplate speed. What were the average speeds of Christopher and of his parents as they drove to the restaurant?

Solution

Footstep 1. Read the problem. Brand sure all the words and ideas are understood.

Describe a diagram to illustrate what it happening. Beneath shows a sketch of what is happening in the example.
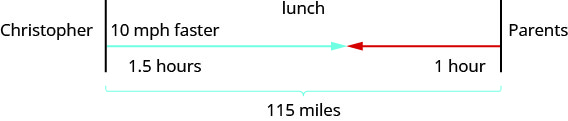
Create a tabular array to organize the information.
Label the columns rate, time, altitude.
List the two scenarios.
Write in the information you know.

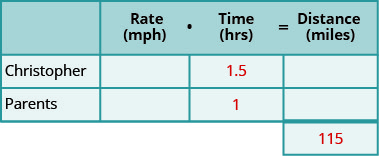
A table with three rows and four columns and an extra cell at the bottom of the fourth column. The first row is a header row and reads from left to right blank, Rate (mph), Time (hrs), and Distance (miles). Below the blank header cell, we have Christopher and Parents. Below the time header cell, we have 1.5 and 1. The extra cell contains 115. The rest of the cells are blank.

Pace 2. Identify what we are looking for.

Nosotros are asked to find the average speeds of Christopher and his parents.

Step three. Name what we are looking for. Choose a variable to correspond that quantity.

Complete the chart.
Utilise variable expressions to stand for that quantity in each row.
We are looking for their average speeds. Let's permit r represent the average speed of the parents. Since the Christopher's speed is 10 mph faster, nosotros stand for that as $r+10.$

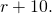
Make full in the speeds into the chart.

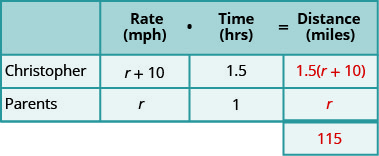
Multiply the rate times the time to go the distance.

Pace 4. Interpret into an equation.

Restate the problem in ane sentence with all the important information.
Then, translate the sentence into an equation.
Again, we demand to identify a relationship between the distances in order to write an equation. Wait at the diagram nosotros created in a higher place and notice the relationship between the distance Christopher traveled and the altitude his parents traveled.

The distance Christopher travelled plus the altitude his parents travel must add together up to 115 miles. So we write:

The sentence,

Stride 5. Solve the equation using good algebra techniques.

At present solve this equation.	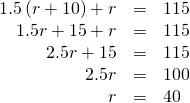$\begin{array}{ccc}\hfill 1.5\left(r+10\right)+r& =\hfill & 115\hfill \\ \hfill 1.5r+15+r& =\hfill & 115\hfill \\ \hfill 2.5r+15& =\hfill & 115\hfill \\ \hfill 2.5r& =\hfill & 100\hfill \\ \hfill r& =\hfill & 40\hfill \end{array}$
	So the parents' speed was 40 mph.
Christopher'southward speed is 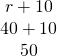$r+10$ .	$\begin{array}{c}\hfill r+10\hfill \\ \hfill 40+10\hfill \\ \hfill 50\hfill \end{array}$
	Christopher's speed was 50 mph.

Step half-dozen. Bank check the answer in the problem and brand sure it makes sense.

Christopher drove	$\begin{array}{ccc}\text{50 mph (1.5 hours)}\hfill & =\hfill & \text{75 miles}\hfill \end{array}$
His parents collection	$\begin{array}{ccccc}& & \text{40 mph (1 hours)}\hfill & =\hfill & \underset{\text{_______}}{\text{40 miles}}\hfill \\ & & & & \text{115 miles}\hfill \end{array}$

Footstep vii. Answer the question with a complete sentence.

Christopher's speed was 50 mph.
His parents' speed was 40 mph.

Carina is driving from her home in Anaheim to Berkeley on the same solar day her blood brother is driving from Berkeley to Anaheim, and so they determine to run across for luncheon forth the way in Buttonwillow. The distance from Anaheim to Berkeley is 410 miles. It takes Carina 3 hours to become to Buttonwillow, while her brother drives four hours to get in that location. The average speed Carina's brother collection was 15 miles per hour faster than Carina's average speed. Discover Carina's and her brother's average speeds.

Carina 50 mph, brother 65 mph

Ashley goes to college in Minneapolis, 234 miles from her home in Sioux Falls. She wants her parents to bring her more winter clothes, so they determine to meet at a restaurant on the route between Minneapolis and Sioux Falls. Ashley and her parents both collection 2 hours to the restaurant. Ashley's average speed was vii miles per hour faster than her parents' average speed. Find Ashley's and her parents' average speed.

parents 55 mph, Ashley 62 mph

As yous read the side by side instance, think almost the relationship of the distances traveled. Which of the previous ii examples is more similar to this situation?

2 truck drivers exit a rest area on the interstate at the same time. 1 truck travels e and the other one travels west. The truck traveling westward travels at lxx mph and the truck traveling east has an average speed of 60 mph. How long will they travel earlier they are 325 miles apart?

Solution

Stride 1. Read the problem. Brand sure all the words and ideas are understood.

Draw a diagram to illustrate what information technology happening.
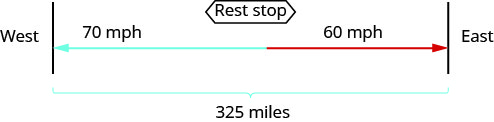
Create a table to organize the information.

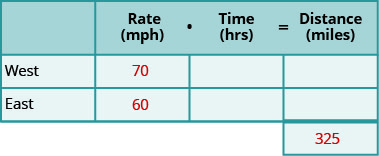
A table with three rows and four columns and an extra cell at the bottom of the fourth column. The first row is a header row and reads from left to right blank, Rate (mph), Time (hrs), and Distance (miles). Below the blank header cell, we have West and East. Below the rate header cell, we have 70 and 60. The extra cell contains 325. The rest of the cells are blank.

Footstep ii. Identify what we are looking for.

Nosotros are asked to find the amount of time the trucks will travel until they are 325 miles apart.

Pace three. Proper noun what we are looking for. Cull a variable to stand for that quantity.

Nosotros are looking for the time travelled. Both trucks will travel the same corporeality of time. Let's call the fourth dimension t. Since their speeds are unlike, they will travel different distances.
Consummate the chart.

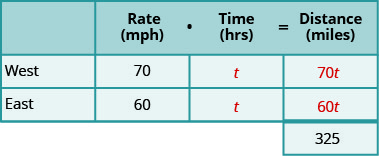
Footstep 4. Translate into an equation.

Nosotros need to find a relation between the distances in order to write an equation. Looking at the diagram, what is the relationship between the distance each of the trucks will travel?
The distance traveled by the truck going west plus the distance travelled by the truck going east must add upward to 325 miles. So we write:

Distance traveled by westbound truck plus distance traveled by eastbound truck equals 325. The first part corresponds to 70t and the second part corresponds to 60.

Step v. Solve the equation using skilful algebra techniques.

Now solve this equation.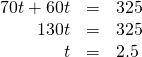

$\begin{array}{ccc}\hfill 70t+60t& =\hfill & 325\hfill \\ \hfill 130t& =\hfill & 325\hfill \\ \hfill t& =\hfill & 2.5\hfill \end{array}$

Then it will take the trucks 2.5 hours to exist 325 miles apart.

Step 6. Bank check the answer in the problem and brand sure it makes sense.

Truck going West

$\begin{array}{ccc}\text{70 mph (2.5 hours)}\hfill & =\hfill & \text{175 miles}\hfill \end{array}$

Truck going Eastward

*** QuickLaTeX cannot compile formula: \begin{array}{ccc}\text{60 mph (2.v hours)}\hfill & =\hfill & \underset{\text{________}}{\text{150 miles}}\hfill \\ & & \text{325 miles}\hfill \end{assortment}  *** Error message: Missing $ inserted. leading text: ...underset{\text{________}}{\text{150 miles}} Missing { inserted. leading text: ...underset{\text{________}}{\text{150 miles}} Missing { inserted. leading text: ...underset{\text{________}}{\text{150 miles}} Missing { inserted. leading text: ...underset{\text{________}}{\text{150 miles}} Missing { inserted. leading text: ...underset{\text{________}}{\text{150 miles}} Missing { inserted. leading text: ...underset{\text{________}}{\text{150 miles}} Missing { inserted. leading text: ...underset{\text{________}}{\text{150 miles}} Missing { inserted. leading text: ...underset{\text{________}}{\text{150 miles}} Missing { inserted. leading text: ...underset{\text{________}}{\text{150 miles}} Missing $ inserted. leading text: ...underset{\text{________}}{\text{150 miles}}

Footstep 7. Answer the question with a complete sentence.

It volition accept the trucks ii.5 hours to be 325 miles autonomously.

Pierre and Monique get out their home in Portland at the same fourth dimension. Pierre drives north on the turnpike at a speed of 75 miles per hour while Monique drives south at a speed of 68 miles per hour. How long volition information technology take them to be 429 miles apart?

3 hours

Thanh and Nhat leave their role in Sacramento at the same time. Thanh drives north on I-5 at a speed of 72 miles per hour. Nhat drives south on I-5 at a speed of 76 miles per hour. How long will it take them to exist 330 miles apart?

ii.2 hours

Matching Units in Problems

It is important to brand sure the units match when we employ the distance rate and time formula. For instance, if the rate is in miles per 60 minutes, then the time must be in hours.

When Katie Mae walks to school, it takes her thirty minutes. If she rides her wheel, it takes her 15 minutes. Her speed is iii miles per 60 minutes faster when she rides her cycle than when she walks. What are her walking speed and her speed riding her cycle?

Solution

First, we describe a diagram that represents the situation to aid usa see what is happening.

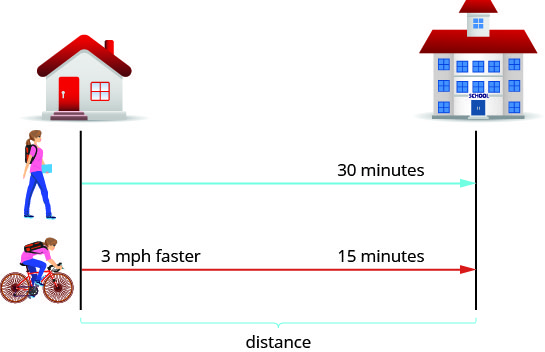
A house and a school are represented by two separate lines. There is a line marked walking from the house to the school that takes 30 minutes. There is a line marked biking from the house to the school that take 15 minutes and is 3 mph faster. The space between the house and school is marked distance.

We are asked to detect her speed walking and riding her bike. Let's call her walking speed r. Since her biking speed is three miles per hour faster, we volition phone call that speed $r+3.$ We write the speeds in the chart.

The speed is in miles per hour, so we need to express the times in hours, besides, in order for the units to be the same. Remember, one 60 minutes is lx minutes. Then:

*** QuickLaTeX cannot compile formula: \begin{array}{}\\ \text{xxx minutes is}\phantom{\rule{0.4em}{0ex}}\frac{30}{lx}\phantom{\rule{0.4em}{0ex}}\text{or}\phantom{\rule{0.4em}{0ex}}\frac{1}{2}\phantom{\rule{0.4em}{0ex}}\text{hour}\hfill \\ \text{15 minutes is}\phantom{\rule{0.4em}{0ex}}\frac{15}{60}\phantom{\rule{0.4em}{0ex}}\text{or}\phantom{\rule{0.4em}{0ex}}\frac{one}{four}\phantom{\rule{0.4em}{0ex}}\text{hour}\hfill \end{assortment}  *** Error message: Missing # inserted in alignment preamble. leading text: $\brainstorm{array}{} Missing $ inserted. leading text: ...is}\phantom{\rule{0.4em}{0ex}}\frac{30}{sixty} Extra }, or forgotten $. leading text: ...is}\phantom{\rule{0.4em}{0ex}}\frac{xxx}{60} Missing } inserted. leading text: ...rule{0.4em}{0ex}}\text{hour}\hfill \\ \text Actress }, or forgotten $. leading text: ...dominion{0.4em}{0ex}}\text{60 minutes}\hfill \\ \text Missing } inserted. leading text: ...rule{0.4em}{0ex}}\text{hour}\hfill \\ \text Actress }, or forgotten $. leading text: ...dominion{0.4em}{0ex}}\text{hour}\hfill \\ \text Missing } inserted. leading text: ...rule{0.4em}{0ex}}\text{hour}\hfill \\ \text Actress }, or forgotten $. leading text: ...rule{0.4em}{0ex}}\text{hour}\hfill \\ \text Missing } inserted.

Next, we multiply rate times time to fill in the distance column.

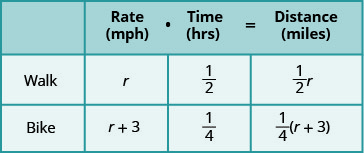
A table with three rows and four columns. The first row is a header row and reads from left to right blank, Rate (mph), Time (hrs), and Distance (miles). Below the blank header cell, we have walk and bike. Below the rate header cell, we have r and r plus 3. Below the time header cell, we have 1/2 and 1/4. Below the distance cell we have 1/2 times r and 1/4 times the quantity (r plus 3).

The equation will come from the fact that the distance from Katie Mae's domicile to her schoolhouse is the same whether she is walking or riding her bike.

So nosotros say:


Translate into an equation.
Solve this equation.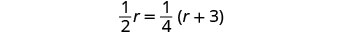
Clear the fractions by multiplying by the LCD of all the fractions in the equation.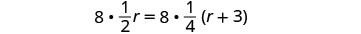
Simplify.	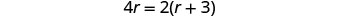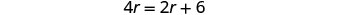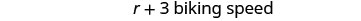6 mph (Katie Mae's biking speed)
Let's check if this works. Walk three mph (0.v hour) = 1.5 miles Cycle 6 mph (0.25 hour) = i.five miles
Yes, either way Katie Mae travels i.five miles to school.	Katie Mae's walking speed is three mph. Her speed riding her bike is six mph.

Suzy takes l minutes to hike uphill from the parking lot to the lookout tower. It takes her 30 minutes to hike back down to the parking lot. Her speed going downhill is 1.2 miles per hour faster than her speed going uphill. Find Suzy'southward uphill and downhill speeds.

uphill 1.8 mph, downhill three mph

Llewyn takes 45 minutes to drive his gunkhole upstream from the dock to his favorite fishing spot. It takes him 30 minutes to drive the gunkhole dorsum downstream to the dock. The boat's speed going downstream is four miles per hr faster than its speed going upstream. Find the boat'south upstream and downstream speeds.

upstream viii mph, downstream 12 mph

In the distance, rate, and time formula, fourth dimension represents the actual corporeality of elapsed time (in hours, minutes, etc.). If a problem gives usa starting and ending times as clock times, nosotros must find the elapsed time in order to use the formula.

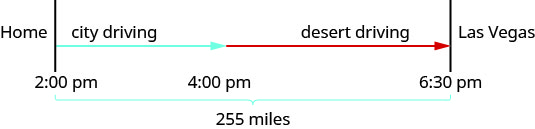
Hamilton loves to travel to Las Vegas, 255 miles from his home in Orange Canton. On his last trip, he left his house at two:00 pm. The beginning part of his trip was on congested metropolis freeways. At iv:00 pm, the traffic cleared and he was able to drive through the desert at a speed 1.75 times faster than when he drove in the congested surface area. He arrived in Las Vegas at 6:thirty pm. How fast was he driving during each role of his trip?

Solution

A diagram will help us model this trip.

Home (2:00 pm) and Las Vegas (6:30 pm) are represented by two separate lines. The space between home and Las Vegas is marked 255 miles. There is an arrow marked city driving from Home/2:00 pm to 4:00 pm. Then there is an arrow marked desert driving from the tip of the previous one at 4:00 pm to Las Vegas/6:30 pm.

Side by side, we create a table to organize the information.

We know the total distance is 255 miles. Nosotros are looking for the rate of speed for each part of the trip. The charge per unit in the desert is 1.75 times the rate in the urban center. If nosotros let $r=$ the rate in the urban center, then the rate in the desert is $1.75r.$

The times here are given as clock times. Hamilton started from domicile at 2:00 pm and entered the desert at 4:thirty pm. Then he spent two hours driving the congested freeways in the urban center. Then he drove faster from 4:00 pm until half-dozen:xxx pm in the desert. So he drove two.5 hours in the desert.

Now, we multiply the rates past the times.

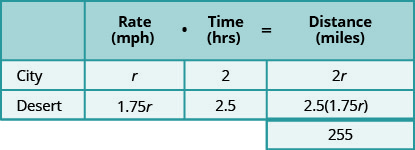
Past looking at the diagram below, we can see that the sum of the distance driven in the city and the distance driven in the desert is 255 miles.


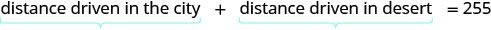Translate into an equation.
Solve this equation.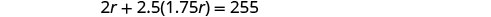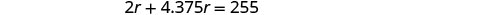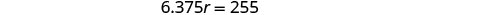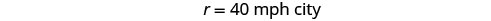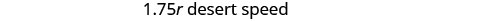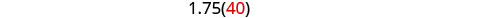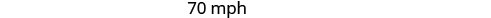
Check.
	Hamilton drove twoscore mph in the metropolis and 70 mph in the desert.

Cruz is training to compete in a triathlon. He left his business firm at 6:00 and ran until 7:30. Then he rode his cycle until 9:45. He covered a total distance of 51 miles. His speed when biking was one.6 times his speed when running. Find Cruz'southward biking and running speeds.

biking 16 mph, running ten mph

Phuong left home on his cycle at x:00. He rode on the flat street until 11:xv, then rode uphill until 11:45. He rode a total of 31 miles. His speed riding uphill was 0.6 times his speed on the flat street. Find his speed biking uphill and on the apartment street.

uphill 12 mph, flat street xx mph

Key Concepts

Distance, Rate, and Time
- D = rt where D = distance, r = rate, t = time
Trouble-Solving Strategy—Distance, Rate, and Time Applications
1. Read the problem. Make sure all the words and ideas are understood.
  Draw a diagram to illustrate what information technology happening.
  Create a table to organize the information: Label the columns rate, time, distance. List the two scenarios. Write in the data y'all know.
2. Identify what nosotros are looking for.
3. Proper noun what we are looking for. Cull a variable to represent that quantity.
  Consummate the chart.
  Utilise variable expressions to represent that quantity in each row.
  Multiply the rate times the fourth dimension to get the distance.
4. Translate into an equation.
  Restate the trouble in one judgement with all the of import information.
  Then, translate the judgement into an equation.
5. Solve the equation using proficient algebra techniques.
6. Check the answer in the problem and make certain information technology makes sense.
7. Answer the question with a complete sentence.

Exercise Makes Perfect

Solve Uniform Move Applications

In the following exercises, solve.

Lilah is moving from Portland to Seattle. It takes her three hours to get by train. Mason leaves the train station in Portland and drives to the train station in Seattle with all Lilah's boxes in his machine. It takes him 2.4 hours to go to Seattle, driving at 15 miles per hour faster than the speed of the train. Find Mason'due south speed and the speed of the railroad train.

Stonemason 75 mph, train 60 mph

Kathy and Cheryl are walking in a fundraiser. Kathy completes the course in 4.8 hours and Cheryl completes the form in 8 hours. Kathy walks two miles per hour faster than Cheryl. Find Kathy'southward speed and Cheryl'southward speed.

Two busses become from Sacramento for San Diego. The express bus makes the trip in half dozen.8 hours and the local bus takes 10.ii hours for the trip. The speed of the express bus is 25 mph faster than the speed of the local bus. Notice the speed of both busses.

express bus 75mph, local 50 mph

A commercial jet and a private airplane wing from Denver to Phoenix. It takes the commercial jet 1.1 hours for the flying, and information technology takes the private airplane 1.8 hours. The speed of the commercial jet is 210 miles per hour faster than the speed of the private airplane. Notice the speed of both airplanes.

Saul drove his truck iii hours from Dallas towards Kansas City and stopped at a truck stop to get dinner. At the truck stop he met Erwin, who had driven iv hours from Kansas Urban center towards Dallas. The distance between Dallas and Kansas Urban center is 542 miles, and Erwin's speed was 8 miles per hr slower than Saul's speed. Find the speed of the two truckers.

Saul 82 mph, Erwin 74 mph

Charlie and Violet met for lunch at a restaurant between Memphis and New Orleans. Charlie had left Memphis and collection 4.8 hours towards New Orleans. Violet had left New Orleans and collection 2 hours towards Memphis, at a speed 10 miles per hour faster than Charlie's speed. The distance between Memphis and New Orleans is 394 miles. Find the speed of the two drivers.

Sisters Helen and Anne live 332 miles apart. For Thanksgiving, they met at their other sister's firm partway betwixt their homes. Helen drove 3.2 hours and Anne collection 2.viii hours. Helen'south average speed was four miles per hour faster than Anne'south. Notice Helen'southward average speed and Anne'due south average speed.

Helen 60 mph, Anne 56 mph

Ethan and Leo start riding their bikes at the opposite ends of a 65-mile bicycle path. After Ethan has ridden 1.5 hours and Leo has ridden 2 hours, they meet on the path. Ethan's speed is six miles per hour faster than Leo's speed. Observe the speed of the ii bikers.

Elvira and Aletheia live three.i miles autonomously on the same street. They are in a study grouping that meets at a coffee shop between their houses. It took Elvira half an hour and Aletheia 2-thirds of an hr to walk to the coffee shop. Aletheia'due south speed is 0.vi miles per 60 minutes slower than Elvira's speed. Discover both women's walking speeds.

Aletheia 2.iv mph, Elvira three mph

DaMarcus and Fabian live 23 miles apart and play soccer at a park between their homes. DaMarcus rode his bike for three-quarters of an hour and Fabian rode his wheel for half an hour to go to the park. Fabian's speed was half-dozen miles per hour faster than DaMarcus' speed. Find the speed of both soccer players.

Cindy and Richard leave their dorm in Charleston at the same time. Cindy rides her bicycle north at a speed of 18 miles per hr. Richard rides his bicycle southward at a speed of 14 miles per hr. How long volition information technology take them to exist 96 miles apart?

3 hours

Matt and Chris leave their uncle'southward house in Phoenix at the aforementioned fourth dimension. Matt drives west on I-60 at a speed of 76 miles per hour. Chris drives e on I-threescore at a speed of 82 miles per hour. How many hours will it take them to be 632 miles apart?

Ii busses leave Billings at the same time. The Seattle autobus heads westward on I-90 at a speed of 73 miles per hour while the Chicago bus heads east at a speed of 79 miles an hour. How many hours will it have them to be 532 miles autonomously?

iii.five hours

Two boats leave the same dock in Cairo at the aforementioned time. 1 heads northward on the Mississippi River while the other heads southward. The northbound boat travels four miles per 60 minutes. The southbound gunkhole goes viii miles per 60 minutes. How long volition it take them to be 54 miles apart?

Lorena walks the path around the park in 30 minutes. If she jogs, information technology takes her xx minutes. Her jogging speed is 1.5 miles per hour faster than her walking speed. Find Lorena'southward walking speed and jogging speed.

walking 3 mph, jogging 4.5 mph

Julian rides his wheel uphill for 45 minutes, and then turns effectually and rides back downhill. It takes him 15 minutes to get dorsum to where he started. His uphill speed is three.2 miles per hr slower than his downhill speed. Find Julian's uphill and downhill speed.

Cassius drives his boat upstream for 45 minutes. Information technology takes him 30 minutes to return downstream. His speed going upstream is iii miles per hour slower than his speed going downstream. Find his upstream and downstream speeds.

upstream half-dozen mph, downstream 9 mph

Information technology takes Darline 20 minutes to drive to work in light traffic. To come home, when there is heavy traffic, it takes her 36 minutes. Her speed in light traffic is 24 miles per hour faster than her speed in heavy traffic. Find her speed in light traffic and in heavy traffic.

At ane:xxx Marlon left his business firm to get to the beach, a altitude of 7.6 miles. He rode his skateboard until 2:15, then walked the residuum of the way. He arrived at the beach at 3:00. Marlon'southward speed on his skateboard is 2.5 times his walking speed. Find his speed when skateboarding and when walking.

skateboarding viii mph, walking 3.ii mph

Aaron left at 9:15 to drive to his mountain motel 108 miles away. He drove on the pike until 10:45, and then he drove on the mountain road. He arrived at 11:05. His speed on the state highway was three times his speed on the mountain road. Discover Aaron's speed on the freeway and on the mountain road.

Marisol left Los Angeles at ii:30 to bulldoze to Santa Barbara, a distance of 95 miles. The traffic was heavy until 3:xx. She drove the rest of the fashion in very low-cal traffic and arrived at 4:20. Her speed in heavy traffic was twoscore miles per 60 minutes slower than her speed in light traffic. Find her speed in heavy traffic and in light traffic.

heavy traffic 30 mph, light traffic 70 mph

Lizette is preparation for a marathon. At 7:00 she left her house and ran until viii:15, then she walked until 11:15. She covered a total altitude of 19 miles. Her running speed was v miles per 60 minutes faster than her walking speed. Notice her running and walking speeds.

Everyday Math

John left his house in Irvine at eight:35 am to drive to a meeting in Los Angeles, 45 miles away. He arrived at the coming together at nine:50. At three:30 pm, he left the coming together and drove home. He arrived home at 5:18.

ⓐ What was his average speed on the drive from Irvine to Los Angeles?
ⓑ What was his average speed on the drive from Los Angeles to Irvine?
ⓓ John drove a total of 90 miles roundtrip. Notice his average speed. (Circular to the nearest tenth.)

Sarah wants to arrive at her friend's wedding at three:00. The distance from Sarah's firm to the hymeneals is 95 miles. Based on usual traffic patterns, Sarah predicts she tin bulldoze the offset 15 miles at 60 miles per 60 minutes, the next 10 miles at xxx miles per 60 minutes, and the remainder of the drive at 70 miles per hour.

ⓐ How long will it take Sarah to bulldoze the showtime 15 miles?
ⓑ How long will it take Sarah to drive the next x miles?
ⓓ What time should Sarah leave her house?

Writing Exercises

When solving a uniform move trouble, how does cartoon a diagram of the state of affairs help you?

Answers volition vary.

When solving a uniform motion problem, how does creating a table help you?

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

No Alt Text

ⓑ What does this checklist tell you about your mastery of this section? What steps will you have to improve?

murphyindes1973.blogspot.com

Source: https://opentextbc.ca/elementaryalgebraopenstax/chapter/solve-uniform-motion-applications/

How Long Until at Rest Again Math Problem

29 Solve Compatible Motion Applications

Learning Objectives

Solve Uniform Motility Applications

Key Concepts

Exercise Makes Perfect

Everyday Math

Writing Exercises

Self Check

0 Response to "How Long Until at Rest Again Math Problem"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel